뇌의 뉴런에서 영감을 얻은 부분이 있지만, 인공 신경망은 실은 뇌와 아무런 관계가 없다.

인공신경망은 단순한 수학 모델에 불과함

아달린은 입력층과 출력층 두 개의 층으로 구성되어 있지만, 입력층과 출력층 사이의 연결이 하나이기 때문에

단일층(single-layer) 네트워크라고 한다.

다층 퍼셉트론에서 확률적 경사 하강법(Stochastic gradient descent)

확률적 경사 하강법은 하나의 훈련 샘플(온라인 학습) 또는 적은 수의 훈련샘플(미니 배치 학습)을 사용해서 비용을 근사한다.

이를 다층 퍼셉트론에서 구현하면, 학습속도가 빠르며, 들쭉날쭉한 학습 특성이 비선형 활성화 함수를 사용한 다층 신경망을

훈련시킬 때 장점이 된다.

다층 신경망의 비용함수는 하나의 볼록 함수가 아니기 때문에, 확률적 경사 하강법의 잡음은 지역 최솟값을 탈출하는데 도움이 된다.

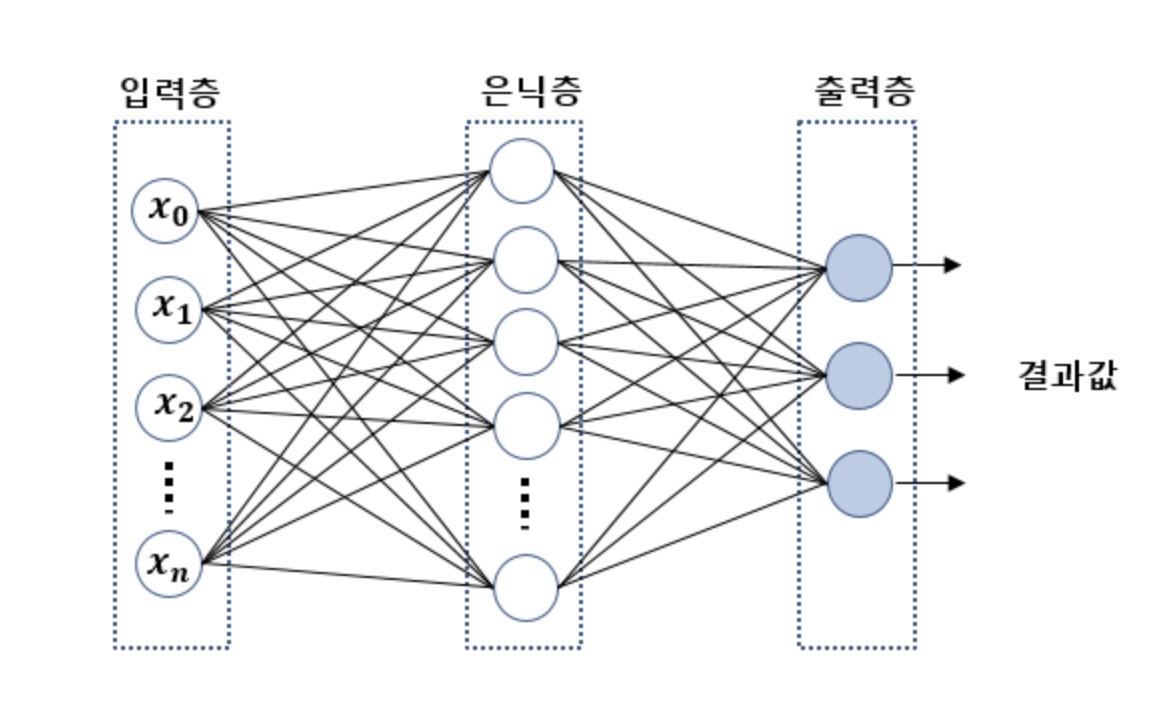
다층 피드 포워드(feedforward)

다층 피드 포워드는 완전 연결 네트워크의 특별한 경우로 다층 퍼셉트론(MuLtilayer Perceptron, MLP)라고 한다.

다층 피드 포워드(다층 퍼셉트론)의 입력층 유닛은 은닉층 유닛과 완전 연결되어 있다.

하나 이상의 은닉츠을 가진 네트워크를 심층 인공 신경망(Deep Artificial Neural Network)라고 한다.

은닉충

깊은 네트워크 구조를 만들기 위해 MLP에 몇 개의 은닉층이든 추가할 수 있다.

신경망의 층과 유닛 개수는 하이퍼파라미터로 교차 검증 기법(CV)를 통해서 최적화 해야한다.

역전파로 계산하는 오차 그레이디언트는 네트워크 층이 추가될수록 더 작아진다. 이런 그레이디언트 소실문제는 모델을 학습하기 어렵게 만든다.

특별한 알고리즘이 이런 심층 신경망 구조를 훈련시키기 위해 개발되었고, 이 것이 딥러닝(Deep Learning)이 되었다.

기존 퍼셉트론과 동일하게 a_0,i(input)과 a_0,h(hidden)은 모두 1이된다.(x_0도 1이였음, w_0(절편)를 위해 만든 유닛)

입력 층의 유닛 활성화는 입력 값에 절편(w_0*x_0)을 더한 것과 같다.

이해 안가면 퍼셉트론 참조할 것_개념 동일함

절편을 위한 표기법

입력 벡터에 1을 추가하고 절편을 포함한 가중치 변수를 사용해서 계산하는 것은 절편 벡터를 분리하고 작업하는 것과 정확히 동일하다.

텐서플로에서는 절편에 대해 별도의 벡터를 사용하는 다층 퍼셉트론을 구현하며, 이는 효율적이고 읽기 좋은 코드구현이 될 수 있다.

가중치 표기법

hidden layer l에 있는 k번 째 유닛, a_k(l) 과 l+1층의 j번 째 유닛, a_j(l+1)로 표기하고 그 사이의 가중치는,

w_k,j(l+1)로 표기한다. -표현법은 다양함

W(h)는 mXd 행렬 모양이다.

d는 은닉 유닛의 개수, m은 절편을 포함한 입력 유닛의 개수

출력층

이진 출력에서는 출력층의 유닛이 하나여도 충분하다.

일반적인 다중 분류를 수행하는 신경망은 OvA(One-versus-All)기법을 적용하면 다중 분류를 수행한다.

n+1개의 입력 유닛, m+1개의 은닉 유닛, 3개의 출력유닛

n-m-3 다층 퍼셉트론(x_0, a_0은 제외함, 절편)

With MLP, function modeling